Como encontrar el limite de una funcion

Como encontrar el limite de una función

como encontrar el limite de una funcion

LOS PUNTOS DE LAS XyY

CRUCE POR LOS EJES DE UNA FUNCION

Para encontrar el cruce en el eje de las abscisas  y ordenadas es decir por donde deberán pasar

 La ecuación será  Y= X+4 Primero se tendrá que observar y tratar de entender que es lo que trasmite la ecuación así como se encuentra  en este caso será lineal será primero sacar el valor de y o por donde pasara la línea en el eje de las ordenadas     

Y a la ecuación donde existe la X se modificara por un cero y quedara de la siguiente manera

Y= 0+4 al realizar quedara por resultado el 4 positivo que es por donde pasara en el eje de las Y

 Para sacar el valor de X la ecuación como esta se modificara  y quedara 0=X+4 al realizar la ecuación el 4 que esta positivo pasar hacer negativo dando como resultado -4 que por donde pasar en el eje de las abscisas

Quedando 4 en ordenadas  Y  -4  en abscisas

 

En ecuaciones cuadráticas el procedimiento cambia un poco la ecuación seria Y=X°+4X +3

 Para sacar el valor de Y será necesario modificar las X por 0

Que quedaría así Y=0° +4(0)+3 al realizar la operación quedaría que Y=3

Ahora para sacar el valor de X se utilizaría la formula general que es la siguiente X=-b+-√(b°-4(a) (c)/2(a) se sustituyen los valores quedando

X=-4+-√4°-4(1) (3)/2(1)

Y LUEGO

X=-4+-√16-12/2

QUEDANDO

-4+-2/2

Lo que quiere decir que tendrá dos valores uno positivó y otro negativo que son los siguientes

-4+2/2=-3

-4-2/2=-1

CRUCE POR LOS EJES DE UNA FUNCION

Para encontrar el cruce en el eje de las abscisas  y ordenadas es decir por donde deberán pasar

 La ecuación será  Y= X+4 Primero se tendrá que observar y tratar de entender que es lo que trasmite la ecuación así como se encuentra  en este caso será lineal será primero sacar el valor de y o por donde pasara la línea en el eje de las ordenadas     

Y a la ecuación donde existe la X se modificara por un cero y quedara de la siguiente manera

Y= 0+4 al realizar quedara por resultado el 4 positivo que es por donde pasara en el eje de las Y

 Para sacar el valor de X la ecuación como esta se modificara  y quedara 0=X+4 al realizar la ecuación el 4 que esta positivo pasar hacer negativo dando como resultado -4 que por donde pasar en el eje de las abscisas

Quedando 4 en ordenadas  Y  -4  en abscisas

 

En ecuaciones cuadráticas el procedimiento cambia un poco la ecuación seria Y=X°+4X +3

 Para sacar el valor de Y será necesario modificar las X por 0

Que quedaría así Y=0° +4(0)+3 al realizar la operación quedaría que Y=3

Ahora para sacar el valor de X se utilizaría la formula general que es la siguiente X=-b+-√(b°-4(a) (c)/2(a) se sustituyen los valores quedando

X=-4+-√4°-4(1) (3)/2(1)

Y LUEGO

X=-4+-√16-12/2

QUEDANDO

-4+-2/2

Lo que quiere decir que tendrá dos valores uno positivó y otro negativo que son los siguientes

-4+2/2=-3

-4-2/2=-1

"Inyectivo, sobreyectivo y biyectivo"

"Inyectivo, sobreyectivo y biyectivo"

"Injectivo" significa que cada elemento de "B" tiene como mucho uno de "A" al que corresponde (pero esto no nos dice que todos los elementos de "B" tengan alguno en "A").

"Sobreyectivo" significa que cada elemento de "B" tiene por lo menos uno de "A" (a lo mejor más de uno).

"Biyectivo" significa inyectivo y sobreyectivo a la vez. Así que hay una correspondencia perfecta "uno a uno" entre los elementos de los dos conjuntos.

Inyectivo

Una función f es inyectiva si, cuando f(x) = f(y), x = y.

Ejemplo: f(x) = x2 del conjunto de los números naturales a es una función inyectiva.

(Pero f(x) = x2 no es inyectiva cuando es desde el conjunto de enteros (esto incluye números negativos) porque tienes por ejemplo

• f(2) = 4 y

• f(-2) = 4)

Nota: inyectiva también se llama "uno a uno", pero esto se confunde porque suena un poco como si fuera biyectiva.

Sobreyectivo (o también "epiyectivo")

Una función f (de un conjunto A a otro B) es sobreyectiva si para cada y en B, existe por lo menos un x en Aque cumple f(x) = y, en otras palabras f es sobreyectiva si y sólo si f(A) = B.

Así que cada elemento de la imagen corresponde con un elemento del dominio por lo menos.

Ejemplo: la función f(x) = 2x del conjunto de los números naturales al de los números pares no negativos es sobreyectiva.

Sin embargo, f(x) = 2x del conjunto de los números naturales a no es sobreyectiva, porque, por ejemplo, ningún elemento de va al 3 por esta función.

Biyectiva

Una función f (del conjunto A al B) es biyectiva si, para cada y en B, hay exactamente un x en A que cumple que f(x) = y

Alternativamente, f es biyectiva si es a la vez inyectiva y sobreyectiva.

Ejemplo: La función f(x) = x2 del conjunto de números reales positivos al mismo conjunto es inyectiva y sobreyectiva. Por lo tanto es biyectiva.

(Pero no desde el conjunto de todos los números reales porque podrías tener por ejemplo

• f(2)=4 y

• f(-2)=4)

DESIGUALDADES E INTERVALOS

1. INTERVALOS: Son regiones comprendidas entre dos números reales.

En general, si los extremos pertenecen al intervalo, se dice que cerrado,

si por el contrario no pertenecen al intervalo, se dice que es abierto.  Si

uno de extremos pertenece al conjunto y el otro  no, se dice que

semiabierto o semicerrado.

CLASES DE INTERVALOS

COMO CONJUNTO TIPO DE INTERVALO REPRESENTACION

GEOMETRICA

{x / a ≤ x ≤ b} [a,b] CERRADO [                          ]

a                         b

]

{x / a ≤ x ≤ b}

[a,b) SEMICERRADO ALA

IZQUIERDA

[                          )

a                         b

{x / a〈x ≤ b} (a,b] SEMICERRADO A LA

DERECHA

(                          ]

a                         b

{x / a ≤ x ≤ b} (a,b) ABIERTO (                          )

a                         b

{x / x〉a} (a,α) (                        

                         

{x / x ≥ a} [a,α ) [                        

                         

{x / x〈b} (−α,b)                           )

                            b{x / x ≤ b} (α,b]                           ]

                            b

{x / x ∈ℜ} (−α,α)

Ejemplos

Dibujar los siguientes intervalos

1.  [2,5)                     [              )

                                                 5

2. (− 6,3 )           (                      )

                                                 6

3. {x ≤ 4}                               ]

                                             4

4.{x 〉 − 3}       (                  

                                           

  0

R

   0

2

   0

-3

   0

0

-35.[− 6,1 ]             [                      ]

DESIGUALDADES

1. INTRODUCCION

ORDEN DE LA RECTA NUMERICA

Decir que a〈b, significa que a está a la izquierda  de b, en la recta numérica

_______________a_____________________b________________R Si   a〈b ⇔ b − a〉0,es decir, que el conjunto de los números reales es un

conjunto ordenado.

PROPIEDADES DE LAS IGUALDADES

Si a, b y c  son números reales

1. TRICOTOMIA

Si a y b son número reales, se cumple una y solo una de las siguientes

propiedades:

a〈b o a = b o a〉b

2. TRANSITIVA

Si a〉b, y b〉c ⇒ a〉c

Ejemplo

12〉8 , y , 8〉5 ⇒ 12〉5

3. ADITIVA

Si a〉b ⇒ a + c 〉 b + c

Ejemplo

Si 9 〉 2, entonces, 9 + 5 〉 2 + 5 ⇒ 14 〉 7

4. MULTIPLICATIVA a) Si c 〉 o, se cumple que

Si a 〉 b ⇒ a.c 〉 b.c

Ejemplo: Sea   8 〉 − 2 y c = 4 ⇒ 8.4 〉 − 2.4

⇒ 32 〉 − 8

b) Si a 〉 b ⇒ a.c 〈 b.c

Ejemplo: Si − 3 〉 − 7 ⇒ (− 3)(− 5) 〈 (− 7)(− 5)

                             

                                      ⇒15 〈 35

5. Si a〉b y c〉d ⇒ a + c 〉 b + d

Ejemplo:  Si 8〉5 y 7〉4 ⇒ 8 + 7 〉 5 +1 ⇒ 15〉9

6. Si a〉0 ⇒ − a〈0

Ejemplo:  si 8〉0 ⇒ − 8〈0

7. ,0 0

2

Si a ≠ a 〉

Ejemplos

8 0 8 64 0

2

Si 〉 ⇒ = 〉

7 0 ( 7) 49 0

2

Si − 〈 ⇒ − = 〉8. 0

1

〉0⇒ 〉

a

Si a

Ejemplo

0

7

1

Si 7 〉 0⇒ 〉

9.

c

b

c

a

Si a〉b y c〉 ,0 entonces, 〉

Ejemplo

2 1

5

5

5

10

Si 10〉5 ⇒ 〉 ⇒ 〉

10.

c

b

c

a

Si a〉b y c〈o ⇒ 〈

Ejemplo:

3 2

8

16

8

24

24 16 〈 ⇒ − 〈 −

−

S

                                                  6

que es una relacion y una funcion

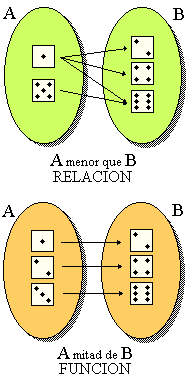
una relación matemática es la correspondencia entre los elementos de dos conjuntos que forman parejas ordenadas y una función matematica es la correspondencia o relación de cada elemento de un conjunto A con un único elemento del conjunto B, es decir,que la Funcion es la Relacion de un elemento de un conjunto con un unico elemento del otro conjunto, por eso no toda Relacion es Funcion, en una grafica si trazas una recta que la corte solo puede tocar un punto de ella.

En matemática, Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto, llamadoRecorrido o Rango, de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango.
Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.

De las definiciones anteriores podemos deducir que todas las funciones son relaciones, pero no todas las relaciones son funciones.

También debemos agregar que toda ecuación es una Relación, pero no toda ecuación es una Función.

Todas las Relaciones pueden ser graficadas en el Plano Cartesiano

Hay casos en que no todos los pares ordenados de un producto cartesiano de dos conjuntos responden a una condición dada. Se llama relación entre los conjuntos A y B a un subconjunto del producto cartesiano A x B. Este puede estar formado por un solo par ordenado, varios o todos los que forman parte de A x B. Si establecemos una relación entre los elementos de un mismo conjunto, existen tres propiedades fundamentales que pueden cumplirse en esa relación: propiedad reflexiva, simétrica y transitiva. Se llama función a una relación en la cual a cada elemento del conjunto de partida le corresponde sólo un elemento del conjunto de llegada.



Origen del cálculo

ORIGEN DEL CÁLCULO. El Cálculo Diferencial se origina en el siglo XVII al realizar estudios sobre el movimiento, es decir, al estudiar la velocidad de los cuerpos al caer al vacío ya que cambia de un momento a otro; la velocidad en cada instante debe calcularse teniendo en cuenta la distancia que recorre en un tiempo infinitesimalmente pequeño. En 1666 Sir Isaac Newton (1642-1727), fue el primero en desarrollar métodos matemáticos para resolver problemas de esta índole. Inventó su propia versión del cálculo para explicar el movimiento de los planetas alrededor del Sol. Newton concibió el llamado Método de las Fluxiones, considerando a la curva como la trayectoria de un punto que fluye; denomina “momentum” de la cantidad de fluente al arco mucho muy corto, recorrido en un tiempo excesivamente pequeño, llamando la “razón del momentum” al tiempo correspondiente es decir, la velocidad. Los orígenes del cálculo se remontan unos 2500 años por lo menos, hasta los antiguos griegos, quienes hallaron áreas aplicando el “método de agotamiento”. El Cálculo Infinitesimal es la rama de las matemáticas que comprende el estudio y aplicaciones del Cálculo Diferencial e Integral. El Cálculo es la matemática del cambio: velocidades y aceleraciones. Cálculo es también la matemática de rectas tangentes, pendientes, áreas, volúmenes, longitudes de arco, centroides, curvaturas y otros diversos conceptos que han hecho que los científicos, ingenieros y economistas puedan modelar situaciones de la vida real. El cálculo es fundamentalmente diferente de las matemáticas que hayas estudiado con anterioridad. Aunque las matemáticas previas al cálculo también versan sobre velocidades, aceleraciones, rectas tangentes, etc., aquí se tiene una diferencia fundamental entre las matemáticas previas y el propio cálculo: las matemáticas previas al cálculo son más estáticas, en tanto que el cálculo es más dinámico. El cálculo se interesa en el cambio y en el movimiento; trata de cantidades que se aproximan a otras cantidades. Podríamos definir al Cálculo como la parte de las matemáticas que trata con límites.